| Issue |
MATEC Web Conf.
Volume 355, 2022
2021 International Conference on Physics, Computing and Mathematical (ICPCM2021)
|
|
|---|---|---|
| Article Number | 02003 | |
| Number of page(s) | 6 | |
| Section | Mathematical Science and Application | |
| DOI | https://doi.org/10.1051/matecconf/202235502003 | |
| Published online | 12 January 2022 | |
Several generalizations on Wolstenholme Theorem
Department of electronic and information engineering, Bozhou University 236800, China
* Corresponding author: zhuyy@hfuu.edu.cn
This paper generalizes Wolstenholme theorem on two aspects. The first generalization is a parameterized form: let p > k + 2, k ≥ 1, ∀t ∈ ℤ, then
The second generalization is on composite number module:
Let 1overa be the x in congruent equation ax ≡ 1(mod m)(1 ≤ x < m),
if m ≥ 5, then
Where φ(x) is Euler function , μ(x) is Möbius function.
Key words: Wolstenholme theorem / Congruent / Composite number module / Möbius transform
© The Authors, published by EDP Sciences, 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




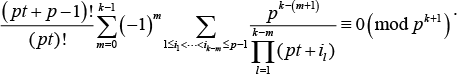
![$$\matrix{ {\sum\limits_{\scriptstyle (k,m) = 1, \hfill \atop \scriptstyle 1 \le j \le m \hfill} {{{\left( {{1 \over k}} \right)}^2}} } \hfill & \equiv \hfill & {{m \over 6}[2m\varphi (m) + \prod\limits_{p|m} {(1 - p)]{{(\bmod m)}^{\;;}}} } \hfill \cr {\sum\limits_{\scriptstyle (k,m) = 1, \hfill \atop \scriptstyle 1 \le j \le m \hfill} {{{\left( {{1 \over k}} \right)}^3}} } \hfill & \equiv \hfill & {{{{m^2}} \over 4}[m\varphi (m) + \prod\limits_{p|m} {(1 - p)](\bmod m){\;^;}} } \hfill \cr {\sum\limits_{\scriptstyle (k,m) = 1, \hfill \atop \scriptstyle 1 \le j \le m \hfill} {{{\left( {{1 \over k}} \right)}^4}} } \hfill & \equiv \hfill & {{m \over {30}}[6{m^3}\varphi (m) + 10{m^2}\prod\limits_{p|m} {(1 - p) - \prod\limits_{p|m} {(1 - {p^3})](\bmod m){\;^;}} } } \hfill \cr {\sum\limits_{\scriptstyle (k,m) = 1, \hfill \atop \scriptstyle 1 \le j \le m \hfill} {{{\left( {{1 \over k}} \right)}^r}} } \hfill & \equiv \hfill & {{m^r}\sum\limits_{d|m} {\mu (d){{\left( {{m \over d}} \right)}^{ - r}}\sum\limits_{k = 1}^{{m \over d}} {{k^r}(\bmod m){\;^.}} } } \hfill \cr } $$](/articles/matecconf/abs/2022/02/matecconf_icpcm2022_02003/matecconf_icpcm2022_02003-eq3.gif)